Question

Please help!!! Select the quadratic equation that has no real solution.

Answer 1

`25x^2-10x+4`

Explanation:

You can use the quadratic formula to determine if a quadratic equation has real or imaginary solutions. The quadratic formula is:
`x=(-b\pm√(b^2-4ac))/(2a)`. What really matters in this case is the discriminant, which is the stuff under the radical which is:
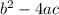`b^2-4ac`. This is because the solutions are only imaginary, if the discriminant is negative, because then you would be taking the square root of a negative number. So let's look through each example:

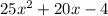`25x^2+20x-4`; a=25, b=20, c-4:
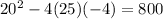`20^2-4(25)(-4) = 800`. By examining this one example, it's important to note, if you have one negative number as a or c, then it cancels out the negative sign in the -4, and it becomes positive. So let's look at examples where a or c doesn't equal a negative number OR both a and c equal negative, that way they cancel out and over -4ac is still negative.

`25x^2-10x+4`; a=25, b=-10, c=4. In this case both a and c are positive so -4ac will remain negative. This gives you:
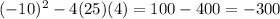`(-10)^2-4(25)(4) = 100-400 = -300`. So this has a negative discriminant meaning it will have no real solution but rather imaginary solutions