Answer:
As per the statement:
The path that the object takes as it falls to the ground can be modeled by:
h =-16t^2 + 80t + 300
where
h is the height of the objects and
t is the time (in seconds)
At t = 0 , h = 300 ft
When the objects hit the ground, h = 0
then;
-16t^2+80t+300=0
For a quadratic equation: ax^2+bx+c=0 ......[1]
the solution for the equation is given by:
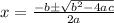
On comparing the given equation with [1] we have;
a = -16 ,b = 80 and c = 300
then;
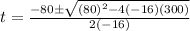


Simplify:
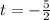 = -2.5 sec and
= -2.5 sec and
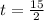 = 7.5 sec
= 7.5 sec
Time can't be in negative;
therefore, the time it took the object to hit the ground is 7.5 sec