Answer:
![a\in (-\infty,1]\cup [3,\infty).](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ksypgj5grg07mcl7vdqes0qi89eoyn137n.png)
Explanation:
Consider the function
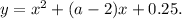 This function represents the parabola with branches that go in positive y-direction (because the leading coefficient is 1>0).
This function represents the parabola with branches that go in positive y-direction (because the leading coefficient is 1>0).
The disriminant of this quadratic function is

When the discriminant is ≥0, the quadratic function will take nonnegative values, thus,
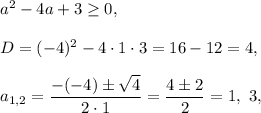
then
![(a-1)(a-3)\ge 0,\\ \\a\in (-\infty,1]\cup [3,\infty).](https://img.qammunity.org/2020/formulas/mathematics/middle-school/lnpisrt9rtihnyf4zohv0xi84nua2arq5a.png)