Question

For what values of a, values of the function y=x2+(a−2)x+0.25 are nonnegative?

Answer 1

`a\in (-\infty,1]\cup [3,\infty).`

Explanation:

Consider the function
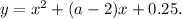`y=x^2+(a-2)x+0.25.` This function represents the parabola with branches that go in positive y-direction (because the leading coefficient is 1>0).

The disriminant of this quadratic function is

`D=(a-2)^2-4\cdot 1\cdot 0.25=a^2-4a+4-1=a^2-4a+3.`

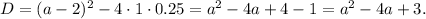
When the discriminant is ≥0, the quadratic function will take nonnegative values, thus,

`a^2-4a+3\ge 0,\\ \\D=(-4)^2-4\cdot 1\cdot 3=16-12=4,\\ \\a_(1,2)=(-(-4)\pm √(4))/(2\cdot 1)=(4\pm 2)/(2)=1,\ 3,`

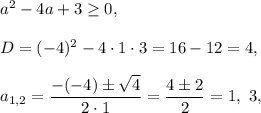
then

`(a-1)(a-3)\ge 0,\\ \\a\in (-\infty,1]\cup [3,\infty).`