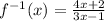Answer:
Given the function:
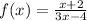
Step 1: Replace f(x) by y;
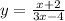
Step 2: Interchange the variables x and y.
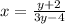
Step 3: Solve for y in terms of x;
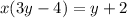
Using distributive property:
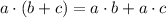
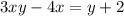
Add 4x to both sides we get;
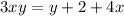
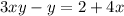
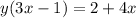
⇒
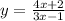
Step 4: Replace y with
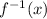
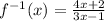
Therefore, the inverse operation of a given function is: