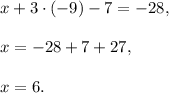Answer:
x=6,
y=-9,
z=7
Explanation:
Rewrite the second equation in the first place
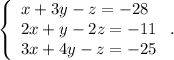
Multiply the first equation by 2 and subtract the second and then multiply the first equation by 3 and subtract the third:
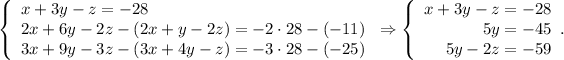
Write the variable y into the third column:
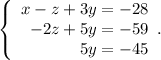
From the last equation
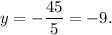
Substitute it into the previous equation:
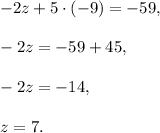
Substitute both y and z into the first equation: