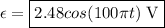Question

Here, a long solenoid of 20000 turns/meter and r=2 cm is oriented along the z-axis (outer circle). There is a small coil of 10 loops of wire of radius 1 cm concentric with the solenoid and lying in the x-y plane (inner circle). An alternating current of magnitude 10 A switches direction every 0.01 seconds in the solenoid. What is the magnitude of the EMF generated in the small loop, in Volts?

Answer 1

Hello!

Recall that the magnetic field produced by a solenoid with a time-varying current is given by:

`B(t) = \mu_0 ni(t)`

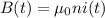
`B(t)` = time-varying magnetic field (T)

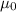`\mu_0` = Permeability of free space (4π × 10⁻⁷ Tm/A)

`n` = number of turns/meter (20000)

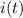`i(t)` = time-varying current

**Since we have AC current, we can use a sinusoidal function to represent the current.

Let's now figure out the expression for the current.

The typical format of a sinusoidal function for current is:

`i(t) = Asin(\omega t + \phi)`

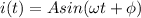
A = amplitude (max current, 10 A)
ω = angular frequency (rad/sec)
φ = phase shift (we will assume there is not one since it is not given.)

We are also assuming we are starting from t = 0 s.

Now we need to solve for the angular frequency to complete our equation.

If the current changes direction every 0.01 seconds, that means that the PERIOD of the current is double this (aka, how long it takes for the current to repeat the same magnitude and direction).

Think about AC current like an oscillating mass on a spring. When the current changes directions, (every 0.01 sec), there is momentarily no current (temporarily no moving charge). The peak current will occur at the halfway point between each change in direction, or every 0.005 sec. Additionally, using this analogy, the mass on a spring changes direction TWICE before it returns to its original position, which is why our period here is double the time it takes for the current to switch directions.

So:

`T = 2(0.01) = 0.02`

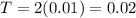
Now, we can convert from period to angular frequency.

`\omega = (2\pi)/(T) = (2\pi)/(0.02) = 100\pi`

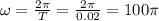
We have the current equation as:

`i(t) = 10sin(100\pi t)`

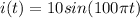
So, our magnetic field produced by the solenoid will be:

`B(t) = (4\pi *10^(-7))(20000)(10sin(100\pi t) )= 0.251sin(100\pi t)`

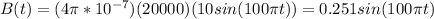
Since we have that figured out, we can use Faraday's Law to find the induced emf:

`\epsilon = -N (d\Phi_B)/(dt)`

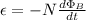
ε = Induced EMF (V)
N = number of loops in COIL (10 loops)

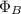`\Phi_B` = Magnetic Flux (Wb)

The area of the coil is constant so we can rewrite the equation as:

`\epsilon = -N * A(dB)/(dt)`

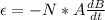
Where 'A' is the cross-sectional area of the COIL.

Let's calculate that:

`A = \pi (0.01^2) = 0.000314 m^2`

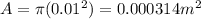
Now, let's calculate the induced emf. Using our equation for 'B' we got earlier:

`B(t) = 0.251sin(100\pi t)\\\\(dB)/(dt) = (100\pi)(0.251)cos(100\pi t) = 78.957cos(100\pi t)`

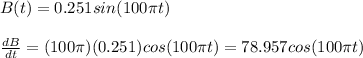
Combining this into Faraday's equation:

`\epsilon = -N * A(dB)/(dt)\\\\\epsilon = -(10)(0.000314)(78.957cos(100\pi t) = -2.48cos(100\pi t)`

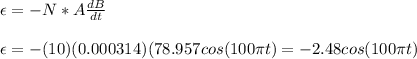
The magnitude is the absolute value, so:

`\epsilon = \boxed{2.48cos(100\pi t) \text{ V}}`