Answer:
1st blank: ∠4≅∠1 and ∠3≅∠2
2nd blank: Angle-Angle similarity postulate
3rd blank: Substitution property of equality.
Explanation:
Consider the provided figure.
Statement Reason
ΔACE, BD║AE Given
∠4≅∠1 and ∠3≅∠2 Corresponding angle postulate
ΔACE
 ΔBCD Angle-Angle similarity postulate
ΔBCD Angle-Angle similarity postulate
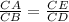 Definition of similar triangles
Definition of similar triangles
CA=CB+BA and CE=CD+DE Segment addition postulate
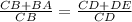 Substitution property of equality.
Substitution property of equality.
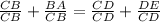 Addition of fractions.
Addition of fractions.
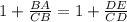 Simplification of fractions
Simplification of fractions
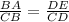 Subtraction property of equality.
Subtraction property of equality.