Question

Drag an expression or phrase to each box to complete the proof.

Answer 1

<BAD ≅ <CFD Alternate interior angles theorem

<ADB ≅ <CDF Vertical angles are congruent

Δ ADB ≈ Δ FDC Angle angle similarity postulate

Answer 2

a)
`\angle BAD = \angle CFD`

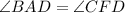
Since we are given that AB || CF

So,
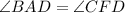`\angle BAD = \angle CFD` (Alternate interior angles)

b)
`\angle ADB = \angle CDF`

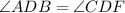
Since they are vertical angles , So, they are congruent

c)ΔADB ≈ΔFDC

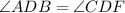`\angle ADB = \angle CDF` (vertical angles)

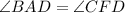`\angle BAD = \angle CFD` (Alternate interior angles)

`\angle ABD = \angle FCD` (Alternate interior angles)

So, ΔADB ≈ΔFDC (By angle angle similarity postulate )