Answer:
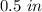

Explanation:
we have
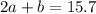
Verify each case
case A)
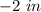
this length does not make sense for a possible value of b
case B)
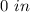
this length does not make sense for a possible value of b
case C)
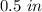
Find the value of a
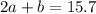
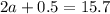
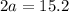
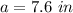
Verify the triangle inequality theorem
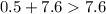 -----> is true
-----> is true
 -----> is true
-----> is true
therefore
this length does make sense for a possible value of b
case D)

Find the value of a
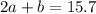
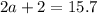
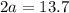
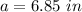
Verify the triangle inequality theorem
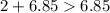 -----> is true
-----> is true
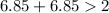 -----> is true
-----> is true
therefore
this length does make sense for a possible value of b
case E)
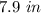
Find the value of a
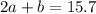

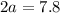
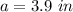
Verify the triangle inequality theorem
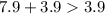 -----> is true
-----> is true
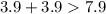 -----> is not true
-----> is not true
therefore
this length does not make sense for a possible value of b