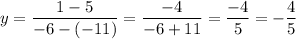Answer:
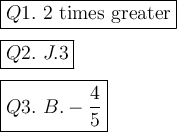
Explanation:
The slope-intercept form of an equation of a line:

m - slope
b - y-intercept
The formula of a slope:
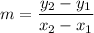
Q1.
We have the equation of a line p in the standard form
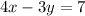
Convert to the slope-intercept form:
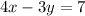 subtract 3x from both sides
subtract 3x from both sides
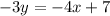 divide both sides by (-3)
divide both sides by (-3)
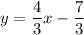
The slope

From the table we have the points (4, 3) and (7, 5). Calculate the slope of line q:
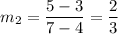
Divide the slope of p by the slope of q:
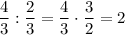
Q2.
Parallel line have the same slope. Therefore, if we have the equation of the line in the slope-intercept form, then we have the slope:
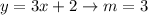
Q3.
Parallel line have the same slope.
Calculate the slope from given points (-11, 5) and (-6, 1):