Question

Tangent (π- α) × cos (π/2 +α) > 0.

The answer is that cos α < 0. Can someone explain why?

Answer 1

Supplementary angles have opposite tangents

tan(π - a) = - tan a

Adding π/2 turns a cosine into a negated sine.

cos(π/2 + a) = - sin a

These are easily shown by the various sum angle formulas; I won't bother here.

`\tan(\pi - a) \cos(\pi/2 + a) = (- \tan a)(- \sin a) = ( \sin a )/( \cos a ) \ \sin a = ( \sin^2 a)/(\cos a)`

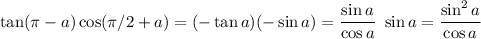
The numerator is never negative so if the whole thing is positive so is the denominator:

`\cos a > 0`

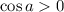
That's the opposite conclusion to the question but I think it's right. Let's check a=π/4.

tan(π - π/4) = tan(3π/4) = -1

cos(π/2 + π/4) = cos(3π/4) = -1/√2

The product is positive.

So is cos(π/4).

I'm right.