Supplementary angles have opposite tangents
tan(π - a) = - tan a
Adding π/2 turns a cosine into a negated sine.
cos(π/2 + a) = - sin a
These are easily shown by the various sum angle formulas; I won't bother here.
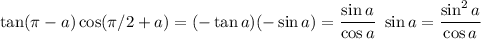
The numerator is never negative so if the whole thing is positive so is the denominator:
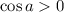
That's the opposite conclusion to the question but I think it's right. Let's check a=π/4.
tan(π - π/4) = tan(3π/4) = -1
cos(π/2 + π/4) = cos(3π/4) = -1/√2
The product is positive.
So is cos(π/4).
I'm right.