Answer: No, she is not correct.
Explanation:
Since we have given that

First we check the consistency of system of equations:

here ,
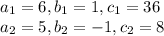
so, it becomes,
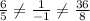
So, it is consistent and it is an intersecting lines.
So, it would have a unique solution.
From Eq(1), we have,

Put it in eq(2), we have

So, x=4 and
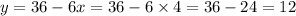
so, the solution point of this line will be (4,12).
No, she is not correct.