Answer:
The average speed for the journey is 6.4 mph.
Explanation:
Given:
If you walk for 45 minutes at a rate of
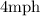 and then run for 30 minutes at a rate of
and then run for 30 minutes at a rate of
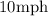 , then how many miles have you gone at the end of one hour and 15 minutes Find the average speed for the journey
, then how many miles have you gone at the end of one hour and 15 minutes Find the average speed for the journey
Step 1 of 1
We can compute the walking distance and running distances separately, then add them.
You walk for 45 minutes, which is
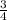 hours, at a rate of
hours, at a rate of
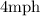 , so the walking distance is
, so the walking distance is
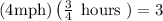 miles. You run for 30 minutes, which is
miles. You run for 30 minutes, which is
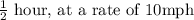 , so the running distance is
, so the running distance is
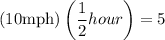 miles.
miles.
So the total distance you cover is 3+5=8 miles.
Now we can also compute the average speed for the journey.
You covered 8 miles in
 hours, so your average speed was
hours, so your average speed was
