Question

A boat is 20 ft away from a point perpendicular to the shoreline. A person stands at a point down the shoreline so that a 60° angle is formed between the closest point to the boat, the person, and the boat. How far is the person from the boat? Draw a picture showing the right triangle. Round your answer to the nearest tenth of a foot.

Answer 1

Distance of the person from the boat is 23.1 feet.

Explanation:

We have,

The distance of the boat from the shoreline = 20 feet.

Angle between the boat and the person = 60°

So, we get the right triangle as shown in the figure.

As, in a right triangle, the angles and sides can be written in trigonometric form.

Thus,
`\sin A=(Perpendicular)/(Hypotenuse)`

i.e.
`\sin 60=(20)/(x)`

i.e.
`0.866=(20)/(x)`

i.e.
`x=(20)/(0.866)`

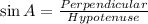
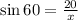
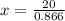
i.e. x = 23.1 feet.

Thus, the distance of the person from the boat is 23.1 feet.