Answer:
The solution set in interval form is
![$\left[(-4)/(3), 4\right]$](https://img.qammunity.org/2023/formulas/mathematics/high-school/5szipeghdlrbugtqwbd3nxb00f3l53nczv.png) .
.
Explanation:
It is given in the question an inequality as
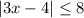 .
.
It is required to determine the solution of the inequality.
To determine the solution of the inequality, solve the inequality
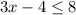 and,
and,
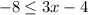 .
.
Step 1 of 2
Solve the inequality
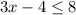
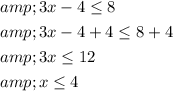
Solve the inequality
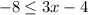 .
.
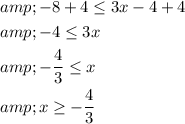
Step 2 of 2
The common solution from the above two solutions is x less than 4 and
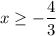 . The solution set in terms of interval is
. The solution set in terms of interval is
![$\left[(-4)/(3), 4\right]$](https://img.qammunity.org/2023/formulas/mathematics/high-school/5szipeghdlrbugtqwbd3nxb00f3l53nczv.png) .
.