Answer:
The linear equation for the line which passes through the points given as (-1,4) and (5,2), is written in the point-slope form as
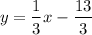 .
.
Explanation:
A condition is given that a line passes through the points whose coordinates are (-1,4) and (5,2).
It is asked to find the linear equation which satisfies the given condition.
Step 1 of 3
Determine the slope of the line.
The points through which the line passes are given as (-1,4) and (5,2). Next, the formula for the slope is given as,
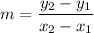
Substitute 2&4 for
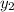 and
and
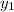 respectively, and
respectively, and
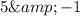 for
for
 and
and
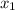 respectively in the above formula. Then simplify to get the slope as follows,
respectively in the above formula. Then simplify to get the slope as follows,
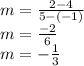
Step 2 of 3
Write the linear equation in point-slope form.
A linear equation in point slope form is given as,
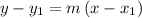
Substitute
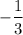 for m,-1 for
for m,-1 for
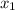 , and 4 for
, and 4 for
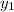 in the above equation and simplify using the distributive property as follows,
in the above equation and simplify using the distributive property as follows,
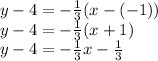
Step 3 of 3
Simplify the equation further.
Add 4 on each side of the equation
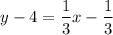 , and simplify as follows,
, and simplify as follows,

This is the required linear equation.