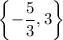Answer:
In interval notation, the solution of |3 x-2|<7 is
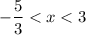 or
or
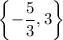 .
.
Explanation:
The given absolute value function is |3 x-2|<7.
It is required to solve the inequality and express the solution using interval notation. -B<x-A<B and solving them separately for x
Step 1 of 3
Given absolute value equation is |3 x-2|<7.
It can be written as -7<3 x-2<7.
To solve for the equality, 3x-2=7 and
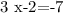
First, solve the equation 3x-2=7, then add 2 on both sides.
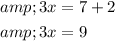
Step 2 of 3
Simplify 3x=9 further, by dividing each side with 3 .

Step 3 of 3
Similarly, 3x-2=-7
From the above term 3x-2=-7,
Add 2 on each side.
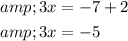
Simplify $3 x=-5$ further, by dividing each side with 3 .
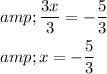
Therefore, the solution is
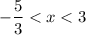 or
or