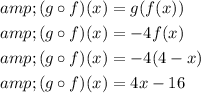Answer:
The value of
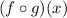 is
is
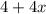 and
and
 is
is
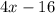 .
.
Explanation:
It is given in the question functions f(x) as 4-x and g(x)=-4x.
It is required to find
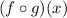 and
and
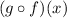 .
.
To find
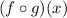 , substitute g(x)=-4x for x in f(x) and simplify the expression.
, substitute g(x)=-4x for x in f(x) and simplify the expression.
To find
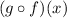 , substitute f(x)=4-x for x in g(x) and simplify the expression.
, substitute f(x)=4-x for x in g(x) and simplify the expression.
Step 1 of 2
Substitute g(x)=-4x for x in f(x) and simplify the expression.
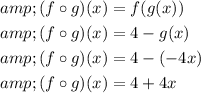
Step 2 of 2
Substitute f(x)=4-x for x in g(x) and simplify the expression.