Question

The distance between New York City, NY, and Louisville, KY is 720 miles. One morning a train traveling 80 mph left from New York. Two hours later a slower train, traveling at 60 mph, left Louisville. How many hours will the slower train travel for before both trains will arrive at the same point?

Answer 1

2 hours

Explanation:

Given : The distance between New York City, NY, and Louisville, KY is 720 miles. One morning a train traveling 80 mph left from New York. Two hours later a slower train, traveling at 60 mph, left Louisville.

To find : How many hours will the slower train travel for before both trains will arrive at the same point?

Solution : Let the distance covered by NY is x

and let the distance covered by KY is y

Total distance covered is
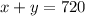`x+y=720` ........[1]

→ New York city,

Distance traveled = x

Speed of the train = 80 mph

Time taken = t+2

Formula is
`\text{Time}=\frac{\text{Distance}}{\text{Speed}}`

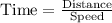
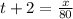`t+2=(x)/(80)` .......[2]

→ Louisville,

Distance traveled = y

Speed of the train = 60 mph

Time taken = t

Formula is
`\text{Time}=\frac{\text{Distance}}{\text{Speed}}`

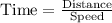
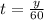`t=(y)/(60)` .......[3]

Put the value of t from [3] into [2]

`(x)/(80)- (y)/(60)=2` ......[4]

Now, we solve equation [1] and [4],

Put the value of y from [1] and put back in [4],
`y=720-x`

`(x)/(80)- (y)/(60)=2`

`(x)/(80)- (720-x)/(60)=2`

`(60x-80(720-x))/(80*60)=2`

`60x-57600+80x=9600`

`140x-57600=9600`

`140x=57600+9600=67200`

`x=(67200)/(140)=480`

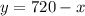
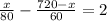
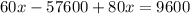
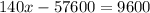
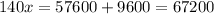
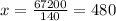
Put x=480 in [1]

`x+y=720`

`480+y=720`

`y=240`

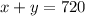
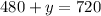
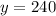
So, The distance covered by train from New York city is x=480 miles

The distance covered by train from Louisville is y=240 miles.

Now put value of y in [3] to get time,

`t=(y)/(60)`

`t=(240)/(60)`

`t=4`

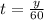
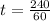
So, The time taken by train from Louisville is 4 hr.

The time taken by train from New York city is t+2=4+2=6 hr.

→ 6-4=2 hours will the slower train travel for before both trains will arrive at the same point.