If triangle CDE is dilated by a scale factor of 1 2 with a center of dilation at the origin, how does the area of C'D'E' compare with the area of CDE?

Question

asked May 4, 2020 74.0k views

2 Answers

Esteban Feldman · Answer 1 · 2020-05-09T07:46:17+0000

Answer: The area of C'D'E' = 1/4 × the area of CDE

Explanation:

Let the coordinates of triangle CDE are
(x_1,y_1) ,
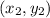(x_2, y_2) and
(x_3,y_3)

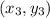
Since, In the dilation about origin by the scale factor k,

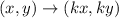
$(x,y) \rightarrow (kx,ky)$

Thus, when triangle CDE is dilated by a scale factor
(1)/(k)

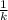
Then the coordinates of triangle C'D'E' are,

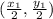((x_1)/(2),(y_1)/(2)) ,
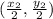((x_2)/(2),(y_2)/(2)) and
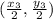
((x_3)/(2),(y_3)/(2))

Since, the area of triangle C'D'E'

=
(1)/(2) [(x_1)/(2) ((y_2)/(2) - (y_3)/(2)) + (x_2)/(2) ((y_3)/(2) - (y_1)/(2))+(x_3)/(2) ((y_1)/(2) - (y_2)/(2))]

=
(1)/(4)[(1)/(2)(x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]

=
$(1)/(4) * \text{ area of triangle CDE}$