Answer:
Option b is correct.
The series 20-15+10-5....is Divergent
Explanation:
Alternating series Test:
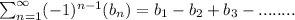
 satisfies:
satisfies:
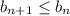 for all n
for all n
Then the series converges,
otherwise diverges.
Given the series: 20-15+10-5....
This is a alternating series:
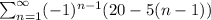

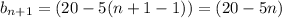
using the alternating series test;
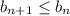 for all n
for all n
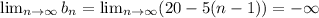
⇒ the series diverges.
therefore, the given series i,e 20-15+10-5.... is divergent.