Question

Determine if the series is convergent or divergent 20-15+10-5....

a) convergent
b) divergent

Answer 1

B

Explanation:

edg 2021

Answer 2

Option b is correct.

The series 20-15+10-5....is Divergent

Explanation:

Alternating series Test:

`\sum_(n=1)^(\infty) (-1)^(n-1) (b_n) =b_1-b_2+b_3-........`

`b_n>0` satisfies:

• 
  `b_(n+1) \leq b_n` for all n

• 
  `\lim_(n\rightarrow \infty) b_n = 0`

Then the series converges,

otherwise diverges.

Given the series: 20-15+10-5....

This is a alternating series:

`\sum_(n=1)^(\infty) (-1)^(n-1) (20-5(n-1))`

`b_n = (20-5(n-1))`

`b_(n+1) = (20-5(n+1-1)) = (20-5n)`

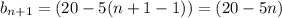
using the alternating series test;

`b_(n+1) \leq b_n` for all n

`\lim_(n\rightarrow \infty) b_n = \lim_(n\rightarrow \infty) (20-5(n-1)) = -\infty`

⇒ the series diverges.

therefore, the given series i,e 20-15+10-5.... is divergent.