Question

Find three consecutive natural numbers if the square of the smallest number is 65 less than the product of the remaining two numbers.

Answer 1

21, 22, and 23

Explanation:

Three consecutive natural numbers can be represented as n, n+1, and n+2.

The square of the smallest number would be
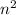`n^2` and its equal to the product of the other two (n+1)(n+2).

So the equation is
`n^2 = (n+1)(n+2) -65\\n^2 = n^2 +n+2n+2-65\\n^2=n^2+3n-63\\0=3n-63\\63=3n\\ 21=n`.

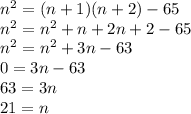If n is 21 then the next numbers are 22 and 23.