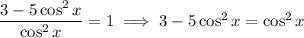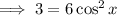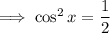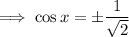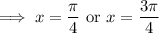By definitions of the (co)tangent and cosecant function,

Turn everything into fractions with common denominators:
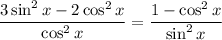
Recall that
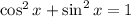 , so we can simplify both sides a bit.
, so we can simplify both sides a bit.
On the left:
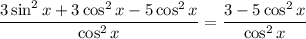
On the right:
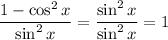
(as long as
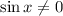 , which happens in the interval
, which happens in the interval
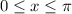 when
when
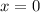 or
or
 )
)
So we have