Question

What is an equation of the line that passes through the point (−4,3) and is perpendicular to the line 4x−3y=3

Answer 1

Steps

• Slope-intercept form: y = mx + b (m = slope, b = y-intercept)
• Standard form: Ax + By = C (A, B, and C are integers and A is nonnegative)

So firstly, we must remember that perpendicular lines have slopes that are negative reciprocals of each other. Now to find the slope of the given line, the easiest method is to convert the standard form equation into slope-intercept. Firstly, subtract both sides by 4x:

`-3y=-4x+3`

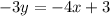
Next, divide both sides by -3:

`y=(4)/(3)x-1`

Now the given line is in slope-intercept form. Given this slope-intercept form, we can see that the slope is 4/3. And with this information, our line's slope is going to be -3/4 (since it's the negative reciprocal).

Now, using the slope-intercept form plug the slope of our new line into the m variable and plug (-4,3) into the x and y variable to solve for b as such:

`3=-(3)/(4)(-4)+b\\3=3+b\\0=b`

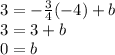
Now with all of our information, the equation for our line is
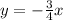`y=-(3)/(4)x` . However, since the given line was in standard form (and it wasn't stated which form the line had to be in) we will put our new line in standard form.

Firstly, add both sides by 3/4x:

`(3)/(4)x+y=0`

Next, we want to make 3/4 an integer. To do this, multiply both sides by 4:

`3x+4y=0`

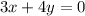
Answer

In short:

• Slope-intercept: y = -3/4x
• Standard Form: 3x + 4y = 0

Answer 2

y = -
`(3)/(4)` x

Explanation:

The equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

rearrange 4x - 3y = 3 into this form

subtract 4x from both sides

- 3y = - 4x + 3 ( divide all terms by - 3 )

y =
`(4)/(3)` x - 1 ← in slope- intercept form

with slope m =
`(4)/(3)`

Given a line with slope m then the slope of a line perpendicular to it is

`m_(perpendicular)` = -
`(1)/(m)` = -
`(1)/((4)/(3) )` = -
`(3)/(4)`

y = -
`(3)/(4)` x + c ← is the partial equation

To find c substitute (- 4, 3) into the partial equation

3 = 3 + c ⇒ c = 3 - 3 = 0

y = -
`(3)/(4)` x ← equation of line