Answer:
The graph touches the x-axis at x=0 and crosses the x-axis at x=5 and x=-2.
Explanation:
We have the following function and we are to solve it for x:
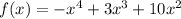
We will put the given function equal to zero and solve it as we know that the function crosses the x-axis when y = 0.
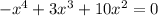
So taking the common terms out:
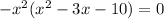
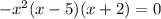

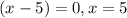

Therefore, the graph touches the x-axis at x=0 and crosses the x-axis at x=5 and x=-2.