Question

Which statement best describes the graph of f(x)=-x^4+3x^3+10x^2

Answer 1

The graph touches the x-axis at x=0 and crosses the x-axis at x=5 and x=-2.

Explanation:

We are given the following function:

`f(x)=-x^4+3x^3+10x^2`

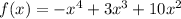
We know that the function crosses the x-axis when y = 0 so we will put this function equal to zero and solve it.

`-x^4+3x^3+10x^2=0`

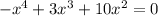
Taking the common out:

`-x^2(x^2-3x-10)=0`

`-x^(2) (x-5)(x+2)=0`

`-x^(2) =0, x=0`

`(x-5)=0, x=5`

`(x+2)=0, x=-2`

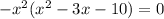
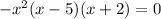
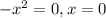
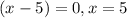
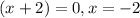
Therefore, the graph touches the x-axis at x=0 and crosses the x-axis at x=5 and x=-2.

Answer 2

option-B

Explanation:

We are given function as

`f(x)=-x^4+3x^3+10x^2`

we know that

Any function touches or crosses x-axis when y-value is 0

so, we can set f(x)=0

and then we can solve for x

`f(x)=-x^4+3x^3+10x^2=0`

now, we can factor it

`-x^2(x^2-3x-10)=0`

`-x^2(x-5)(x+2)=0`

we get

`-x^2=0`

`x=0`

It means that function touches x-axis at x=0

`(x-5)(x+2)=0`

`(x-5)=0`

`x=5`

`(x+2)=0`

`x=-2`

So, function crosses x-axis at x=5 and x=-2

so,

option-B