Question

The hypotenuse and one of the legs of a right triangle form an angle that has a sine of 4/9 . What is the tangent of the angle?

A) 4 (sq rt65)/65
B) 9(sq rt65)/65
C) (sq rt65)/4
D) (sq rt65)/9

Answer 1

A

Explanation:

So by drawing a right triangle, and knowing that Sin of an angle is the opposite over hypotenuse, we know what two of the three sides are. Using the Pythagorean theorem, we know that 4^2+b^2 = 9^2. Since 16+ b^2 = 81, we can solve for be to get b^2 = 65, which means that the missing leg is the square root of 65. Tan of an angle is opposite over adjacent, or 4/square root 65. since square roots can not be in the denominator, multiply by the fraction sq. rt. 65/ sq. rt. 65. After you multiply, you should get the answer of 4(sq.rt. 65)/ 65

Answer 2

(A)
`tanC=(4√(65))/(65)`

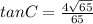
Explanation:

Given: The hypotenuse and one of the legs of a right triangle form an angle that has a sine of
`{(4)/(9)}`.

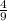To find: The tangent of the angle.

Solution: It is given that hypotenuse and one of the legs of a right triangle form an angle that has a sine of
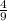`{(4)/(9)}`, that is

AB=4 and AC=9

Now, using Pythagoras theorem, we have

`(AC)^2=(AB)^2+(BC)^2`

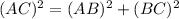
Substituting the given values, we get

`(9)^2=(4)^2+(BC)^2`

`81=16+(BC)^2`

`(BC)^2=65`

`(BC)=√(65)`

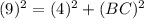
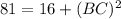
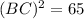
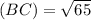
Now, using trigonometry, we have

`tanC=(AB)/(BC)`

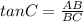
Substituting the given values, we have

`tanC=(4)/(√(65))`

`tanC=(4√(65))/(65)`

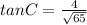
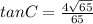
Thus, option A is correct.