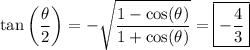Recall the Pythagorean identity,
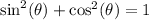
Since
 belongs to Q3, we know both
belongs to Q3, we know both
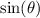 and
and
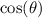 are negative. Then
are negative. Then
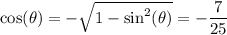
Recall the half-angle identities for sine and cosine,
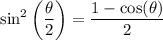
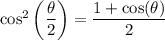
Then by definition of tangent,
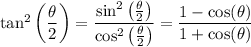
 belonging to Q3 means
belonging to Q3 means
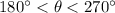 , or
, or
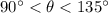 , so that the half-angle belongs to Q2. Then
, so that the half-angle belongs to Q2. Then
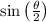 is positive and
is positive and
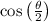 is negative, so
is negative, so
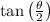 is negative.
is negative.
It follows that