Answer:
53,316,291,173
Explanation:
If these terms F(51) and F(52) follow the Fibonacci sequence, then the rule for the sequence will be,

That means,
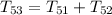
Therefore,
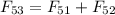
= 20,365,011,074 + 32,951,280,099
= 53,316,291,173
Therefore, addition of these terms will be 53,316,291,173.
This clearly speaks that in the Fibonacci sequence addition of two terms forms the third number of the sequence.