Answer:
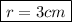
Explanation:
The volume of a cylinder is given by the formula;
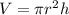
It was given that the volume of the cylinder,
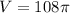 , and its height,
, and its height,
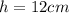
We substitute the given values into the formula to obtain;
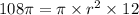
We divide through by
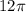 to obtain;
to obtain;
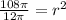
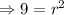
We take the positive square root of both sides to obtain;
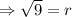

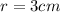
Therefore the length of the cylinder's radius is 3cm.