Question

Given that f(x) = 10x + 45, find f(7)

Answer 1

`\boxed{\bf f(x) = 115}`

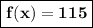
Explanation:

Given polynomial function :-

`f(x) = 10x + 45`

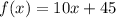
To find :-

`\sf \: f(7)`

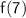
Solution:-

`\sf \implies \: f(x) = 10x + 45`

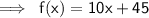
Here, the value of x is 7(given).

So, Substitute the value of x on the RHS and on LHS :-

`\sf \implies{f}(“7”) = 10(“7”) + 45`

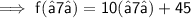
Simplify the RHS:-

Multiply 10 and 7 :-

`\sf \implies{f}(7) = 10 * 7 + 45`

`\sf \implies{f}(7) = 70 + 45`

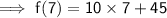
Add 70 and 45 :-

`\sf \implies{f}(7) = 115`

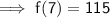
We're done!

Hence, the value of f(7) would be,

`\sf \implies{f}(7) = 115`

`\rule{225pt}{2pt}`

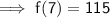
I hope this helps!

Let me know if you have any questions.