Question

Help me solve this!!!

Answer 1

C

Explanation:

Here we can see this is a bit of an trial and error, let's go through the options individually.

To find whether the ordered pair satisfies the equation, we will substitute x and y into the equation. To have the ordered pair to satisfy the equation, the value must be 7.

A) Given x = -5 , y = 3,

`-5x+3y= - 5(-5)+3(3)\\=25+9\\= 34\\34 \\eq 7`

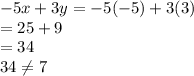
Therefore this pair does not satisfy the equation.

B) Given x = 2, y = -1,

`-5x+3y = -5(2)+3(-1)\\= -10-3\\=-13\\-13 \\eq 7`

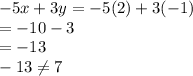
Therefore this pair does not satisfy the equation.

C) Given x = 7, y = 14,

`-5x+3y = -5(7)+3(14)\\= -35 + 42\\= 7`

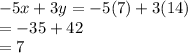
Therefore this pair satisfy the equation.

D) Given x = -2, y =
`-(13)/(5)`,

`-5x+3y = -5(-2)+3(-(13)/(5) )\\=-10-(39)/(5) \\=-17.8 or -17(4)/(5) \\-17.8\\eq 7`

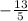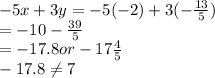
Therefore this pair does not satisfy the equation.