Answer:
0.32
Explanation:
We have been given that at a high school, the probability that a student is a senior is 0.25. The probability that a student plays a sport is 0.20. The probability that a student is a senior and plays a sport is 0.08.
We will use conditional probability formula to solve our given problem.
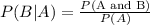 , where,
, where,
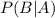 = The probability of event B given event A.
= The probability of event B given event A.
 = The probability of event A and event B.
= The probability of event A and event B.
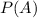 =Probability of event A.
=Probability of event A.
Let A be that the student is senior and B be the student plays a sport.
P(A and B) = Probability that student is a senior and plays a sport.
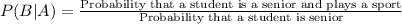
Upon substituting our given values we will get,
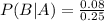

Therefore, the probability that a randomly selected student plays a sport, given that the student is a senior will be 0.32.