Answer:
Volume of the similar sphere be 64 :343 .
Option (D) is correct.
Explanation:
Formula

As given
The volumes of two similar spheres given that the ratio of their radii is 4:7 .
Let us assume that the x be the scalar multiple of the radi .
Radius of first sphere = 4x
Radius of second sphere = 7x
Putting the values in the formula
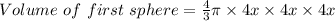

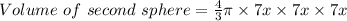
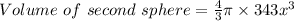
Thus
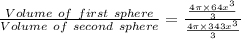
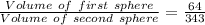
Therefore the ratio of the volume of the similar sphere be 64 :343 .
Option (D) is correct .