Answer:
Explanation:
Given is an algebraic polynomial of degree 5.

Here leading term is p=3 and constant term is q =12
Factors of p are ±1,±2,±3
Factors of q are
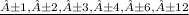
Possible forms of p/q will be the same for any other polynomial of degree 5 with leading term =3 and constant term = 12
Hence any other polynomial

will have same possible zeroes of p/q, when a,b,c are rational.
Hence any polynomial of this type would have the same possible rational roots.