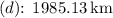the calculated values are approximately:
- Centripetal Acceleration
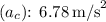
- Time of Turn
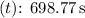
- Distance Covered
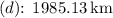
Let's go through each part of the problem:
a. Centripetal Acceleration:
Given that the speed of the airplane v is
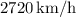 and the radius r is
and the radius r is
 , let's calculate the centripetal acceleration
, let's calculate the centripetal acceleration
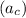 .
.
First, convert the speed from kilometers per hour to meters per second:
![\[ v = 2720 \, \text{km/h} * \frac{1000 \, \text{m}}{1 \, \text{km}} * \frac{1 \, \text{h}}{3600 \, \text{s}} \]\[ v = (2720 * 1000)/(3600) \, \text{m/s} \]](https://img.qammunity.org/2023/formulas/physics/college/skc7rh672vo1pep14vh29ewcvk0ml77dq1.png)
Now, substitute the values into the centripetal acceleration formula:
![\[ a_c = (v^2)/(r) \]\[ a_c = (\left((2720 * 1000)/(3600)\right)^2)/(84 * 10^3) \]](https://img.qammunity.org/2023/formulas/physics/college/3g9amkoscsz6hgs8i4avqa1xmgzd1w6cm6.png)
Calculate
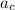 .
.
![\[ v = (2720 * 1000)/(3600) \, \text{m/s} \]\[ a_c = (\left((2720 * 1000)/(3600)\right)^2)/(84 * 10^3) \]\[ a_c \approx ((755.56)^2)/(84 * 10^3) \]\[ a_c \approx (570004.94)/(84 * 10^3) \]\[ a_c \approx 6.78 \, \text{m/s}^2 \]](https://img.qammunity.org/2023/formulas/physics/college/asrytds7olu5ykhixtrdkugj1hncobvzq0.png)
b. Time of Turn:
The time t taken for one complete revolution is given by the formula:
![\[ t = (2 \pi r)/(v) \]](https://img.qammunity.org/2023/formulas/physics/college/12kcuouw4r9zkyes1er5mnefxn0uumq6vf.png)
Substitute the known values into the formula:
![\[ t = (2 \pi * 84 * 10^3)/((2720 * 1000)/(3600)) \]](https://img.qammunity.org/2023/formulas/physics/college/uw4yire3a4thn962gvl5tn28rv6ojxil8m.png)
Calculate t.
![\[ t = (2 \pi * 84 * 10^3)/((2720 * 1000)/(3600)) \]\[ t \approx (2 * 3.1416 * 84 * 10^3)/((2720 * 1000)/(3600)) \]\[ t \approx (527885.76)/(755.56) \]\[ t \approx 698.77 \, \text{s} \]](https://img.qammunity.org/2023/formulas/physics/college/h3xuaxc7ogc2cc11ljp286zq8otbir963j.png)
c. Distance Covered:
The distance d covered during the turn is given by the formula:
![\[ d = vt \]](https://img.qammunity.org/2023/formulas/physics/college/bp4b9356nb22vexrj7cud034ocrns6w6vj.png)
Substitute the known values into the formula:
![\[ d = \left((2720 * 1000)/(3600)\right) * (2 \pi * 84 * 10^3)/((2720 * 1000)/(3600)) \]](https://img.qammunity.org/2023/formulas/physics/college/xfk4oo6g2jsyz6qhbp6saar0gqx078pdvi.png)
Calculate d.
![\[ d = \left((2720 * 1000)/(3600)\right) * (2 \pi * 84 * 10^3)/((2720 * 1000)/(3600)) \]\[ d \approx (755.56 * 2 * 3.1416 * 84 * 10^3)/((2720 * 1000)/(3600)) \]\[ d \approx (1501664.66)/(755.56) \]\[ d \approx 1985.13 \, \text{km} \]](https://img.qammunity.org/2023/formulas/physics/college/n4i4x3gsmk8cn5rd873g1m64x76cw2m1hh.png)
So, the calculated values are approximately:
- Centripetal Acceleration
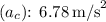
- Time of Turn
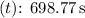
- Distance Covered