Question

1-Suppose the path of a baseball follows the path graphed by the quadratic function ƒ(d) = –0.6d2 + 5.4d + 0.8 where d is the horizontal distance the ball traveled in yards, and ƒ(d) is the height, in yards, of the ball at d horizontal yards. Identify the domain and range that matches this situation

Domain: [0,12.95] horizontal yards, range: [0,9.15] vertical yards
B. Domain: [0,9.15] horizontal yards, range: [0,12.95] vertical yards
C. Domain: [0,12.95] vertical yards, range: [0,9.15] horizontal yards
D. Domain: [0,9.15] vertical yards, range: [0,12.95] horizontal yards



2-Which of the following is the graph of y = (x – 1)2 + 1?

Answer 1

1. The correct option B.

2.The correct option A.

Explanation:

The given function is

`f(d)=-0.6d^2+5.4d+0.8`

Where f(d) is the height of the ball at horizontal distance d.

Put f(d)=0, to find the distance where the ball touch the ground.

`0=-0.6d^2+5.4d+0.8`

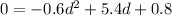
Quadratic formula:

`d=(-b\pm √(b^2-4ac))/(2a)`

Using the quadratic formula we get

`d=(-5.4\pm √((5.4)^2-4(-0.6)(0.8)))/(2(-0.6))`

`d=-0.146,9.146`

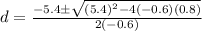
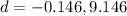
Therefore the ball is in air between d=-0.146 to d=9.146.

The distance can not be negative, therefore the ball remains in the air between d=0 to d=9.146.

`9.146\approx 9.15`

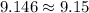
Therefore the correct option is B.

2.

The given equation is

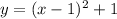`y=(x-1)^2+1` .... (1)

The standard form of parabola is

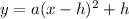`y=a(x-h)^2+h` .... (2)

Where, a is constant and (h,k) is vertex.

On comparing (1) and (2), we get

`a=1`

`h=1`

`k=1`

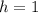
Since the value of a is positive, therefore it is an upward parabola. The vertex of the parabola is (1,1).

Put x=0 in the given equation.

`y=(0-1)^2+1`

`y=1+1=2`

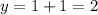
Therefore the y-intercept is (0,2) and option A is correct.