Question

What is the range of the function y =^3 Square root x+ 8?

Answer 1

all real numbers

Explanation:

The range of any odd root function is all real numbers, cube root included.

y = ∛(x+8)

is defined for all values of x. It may take on any value for y.

____

The horizontal scale of the graph is quite large so as to show the vertical extent keeps increasing. (The x-intercept is -8.)

Answer 2

The range of the function is: -∞≤y≤∞.

Explanation:

Consider the provided function

`y=\sqrt[3]{x+8}`

The range of the function is the set of all values which a function can produce or the set of y values which a function can produce after substitute the possible values of x.

The range of a cubic root function is all real numbers.

Now consider the provided function.

`y=\sqrt[3]{x+8}`

The above function can be written as:

`y=(x+8)^{(1)/(3)}`

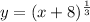
Taking cube on both sides.

`y^3=x+8\\\\x=y^3-8`

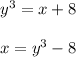
The graph of the function is shown in figure 1:

For any value of x we can find different value of y.

Here, the cube root function can process negative values. Since, the function can produce any values, the range of the given function is -∞≤y≤∞ .

Therefore, the range of the function is: -∞≤y≤∞.