Explanation:
so you have the equation:
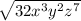 which I'm assuming is what you meant to input. and the next step I'm assuming you wrote:
which I'm assuming is what you meant to input. and the next step I'm assuming you wrote:
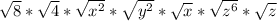 , although I'm not 100% sure, I'm basing this assumption off of step 3. Anyways this will simplify to
, although I'm not 100% sure, I'm basing this assumption off of step 3. Anyways this will simplify to
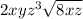 which is correct kind of, but since they were asked to FULLY SIMPLIFY, then it's not completely done. This is because 8 has a factor of 4 which is a perfect square. This is because in step 1, the student rewrote 32 as sqrt(8) * sqrt(4) instead of writing it as sqrt(2) * sqrt(16) which is the greatest factor of 32 that is a perfect square. So they could've either done that in step 1, or they could've realized in step 2, that they can further simplify sqrt(8) and then have a step 3 showing that.
which is correct kind of, but since they were asked to FULLY SIMPLIFY, then it's not completely done. This is because 8 has a factor of 4 which is a perfect square. This is because in step 1, the student rewrote 32 as sqrt(8) * sqrt(4) instead of writing it as sqrt(2) * sqrt(16) which is the greatest factor of 32 that is a perfect square. So they could've either done that in step 1, or they could've realized in step 2, that they can further simplify sqrt(8) and then have a step 3 showing that.