Question

A student submitted the following work that is not correct. Can you find the mistake?

Explain the mistake the student made.
Simplify (assuming all variables are positive): √32x³y²z7
Step 1: √8.4.x².xy².26. z
Step 2: 2xyz³ √8xz

Answer 1

Explanation:

so you have the equation:
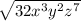`√(32x^3y^2z^7)` which I'm assuming is what you meant to input. and the next step I'm assuming you wrote:
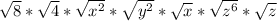`√(8) * √(4) * √(x^2) * √(y^2) * √(x) * √(z^6) * √(z)`, although I'm not 100% sure, I'm basing this assumption off of step 3. Anyways this will simplify to
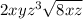`2xyz^3√(8xz)` which is correct kind of, but since they were asked to FULLY SIMPLIFY, then it's not completely done. This is because 8 has a factor of 4 which is a perfect square. This is because in step 1, the student rewrote 32 as sqrt(8) * sqrt(4) instead of writing it as sqrt(2) * sqrt(16) which is the greatest factor of 32 that is a perfect square. So they could've either done that in step 1, or they could've realized in step 2, that they can further simplify sqrt(8) and then have a step 3 showing that.