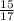Answer:
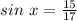
Explanation:
So in this case, it's similar to the previous question you asked, except this time you know cosine, and as you may know cosine is defined as:
 and sine is defined as:
and sine is defined as:
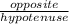 . So all we need to solve for is the opposite side, but since we know two sides, we can solve for the other using the Pythagorean identity:
. So all we need to solve for is the opposite side, but since we know two sides, we can solve for the other using the Pythagorean identity:

Plug in known values:
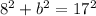
Simplify:
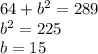
So the opposite side is 15, and the hypotenuse is already given, in this case it's 17 (the denominator of cosine). So plugging this into the definition of sin gives you: