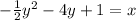Answer:
Explanation:
A parabola has a focus of F(8.5,−4) and a directrix of x=9.5.
General form of horizontal parabola is
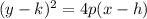
the distance between directrix and focus is the value of p
so p = 8.5 - 9.5 = -0.5
Focus is (h+p , k), given focus is (8.5, -4)
So k = -4 and h+p = 8.5
we know p = -0.5
h +p = 8.5
h - 0.5 = 8.5
so h= 9 and k = -4
vertex is (h,k) that is (9, -4)
Now plug in the value in the general equation
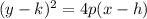 , k= -4, h= 9 , p = -0.5
, k= -4, h= 9 , p = -0.5
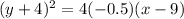
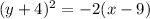
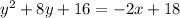
subtract 18 on both sides
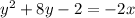
Divide whole equation by -2