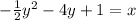Question

A parabola has a focus of F(8.5,−4) and a directrix of x=9.5.

What is the equation of the parabola?

1. 1/2y2+4y−1=x
2 .1/2y2−4y+1=x
3. −1/2y2+4y−1=x
4. −1/2y2−4y+1=x

Answer 1

`-(1)/(2)y^2-4y+1=x`

Explanation:

A parabola has a focus of F(8.5,−4) and a directrix of x=9.5.

General form of horizontal parabola is

`(y-k)^2=4p(x-h)`

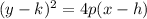
the distance between directrix and focus is the value of p

so p = 8.5 - 9.5 = -0.5

Focus is (h+p , k), given focus is (8.5, -4)

So k = -4 and h+p = 8.5

we know p = -0.5

h +p = 8.5

h - 0.5 = 8.5

so h= 9 and k = -4

vertex is (h,k) that is (9, -4)

Now plug in the value in the general equation

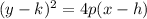`(y-k)^2=4p(x-h)`, k= -4, h= 9 , p = -0.5

`(y+4)^2=4(-0.5)(x-9)`

`(y+4)^2=-2(x-9)`

`y^2+8y+16=-2x+18`

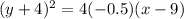
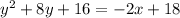
subtract 18 on both sides

`y^2+8y-2=-2x`

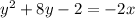
Divide whole equation by -2

`-(1)/(2)y^2-4y+1=x`