Answer:
There are 60 permutations that can be formed from the first five letters of the alphabet.
Explanation:
The number of three letter permutations that can be formed from the first five letters of the alphabet is
 .
.
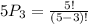
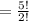
= 60
Hence, there are 60 permutations that can be formed from the first five letters of the alphabet.