Answer:
The volume of a cube is (also known as regular hexahedron) is equal to the length of its edges elevated to the cube (taking into account that in a cube each side and edge has the same size).
In this case we have a first cube (called cube 1) which edges are
 , hence its volume is:
, hence its volume is:
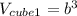
Also we know cube 2 side lengths or edges
 are twice those of cube 1, this means:
are twice those of cube 1, this means:

Therefore the volume of cube 2 is:
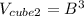
Which is the same as:

Therefore the right answer is B