1. Answer:
From the problem, we have the following statement:
MIKE’S REPAIR SHOP $100 Service Charge plus $65 per hour.
AMY’S AUTO REPAIR $40 Service Charge plus $80 per hour.
We also know that:
Let x = number of hours worked
Let y = total cost to you
So an equation for each repair shop to represent the total cost of a car repair as a function of the number of hours worked can be found as:
For MIKE’S REPAIR SHOP:
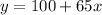
For AMY’S AUTO REPAIR:
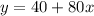
2. Answer:
Let's use substitution method as follows:
1. Write one equation in the form variable =:

Both equations are written in this form.
2. Replace that variable in the other equation:
Let's take MIKE’S REPAIR SHOP equation and replace y in AMY’S AUTO REPAIR equation:

3. Solve:
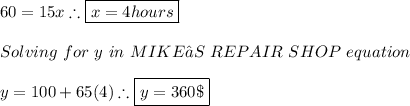
So the point of intersection is:

3. Answer:
The two lines intersect at the point of intersection. This is shown in the first figure below. This figure show two lines, the red line represents Mike's repair shop while the green line represents Amy's auto repair. There you can see that the point (4, 360) is the intersection of these two lines.
4. Answer:
Since you need to get the dent in your car repaired, the context of this problem is to find the best shop to do that. Therefore, the point of intersection tells us that for 4 hours the cost of the two shops will be the same and equal to 360$. So if it would only take 4 hours to get the car repaired you can choose either Mike's repair shop or the Amy's auto repair.
5. Answer:
It is easy to find this answer by taking a look at the second figure. There we have plotted two points with x-coordinate = 3. So you can see that for this value the y-coordinate on the green line is less than the y-coordinate on the red line. This implies that:
Part a. for 3 hours Amy's auto repair would be cheapest.
Part b. The cost would be 280$
6. Answer:
This problem can be solved by taking a look at the third figure. There we have plotted two points with x-coordinate = 6. So you can see that for this value the y-coordinate on the red line is less than the y-coordinate on the green line implying that:
Part a. for 6 hours Mike's repair shop would be cheapest.
Part b. The cost would be 490$
7. Answer:
The answer is Amy's auto repair because the cost to get a car repaired is less up to 4 hours. So this shop encourages customers to use its services with quick repairs at a low cost. So it is obvious that you shall choose Amy's auto repair instead of Mike's repair shop.