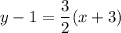Answer:
The required equation is
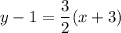
Explanation:
The equation of given line is
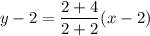
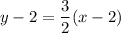
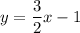
The slope of the given equation is

As we know the slope of parallel line is equal.
Thus, The slope of required line is

Passing point: (-3,1)
Using point slope formula:

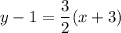
Hence, The required equation is